ワンダーファイ株式会社 Wonderfy Inc.

左辺の"$Value$"は、組織にとって価値であるとみなされる程度を意味しており、これは、資産の増減量やコストの削減量等、特定の客観的な尺度で決められる評価とは異なるものです。つまり、この式は、会社が"$challenge$"に対してどのように価値を見出すかを定義している式です。

"$challenge$"は、「自らの意思で起こした新たな行動の内容」を表すものですが、数学的に考える場合、これは例えば実数を成分とするベクトルで記述されていると考えるとよいでしょう（あるいは、情報処理の考え方に基づいて、テキストデータの組として記述されていると考えてもよいでしょう）。行動の内容をベクトル化する方法については省略しますが、「自らの意思で起こした新たな行動の内容」をベクトルで書き表すことができたとして、それを"$challenge$"と記述するならば、関数$f$は、ベクトルを入力とし、そのベクトルが表す「行動の内容」がもたらした結果について、ある特定の尺度において決定される評価を（正負を含めて）アウトプットする関数です。ここでいう"ある特定の尺度"は、勿論、左辺で述べられる"$Value$"とは異なる尺度であり、例えば営業利益の尺度や、タスクがどれだけこなせたかを表す尺度、コストの削減量の尺度、出来上がったものの商品としての善し悪しの尺度、世間一般において成功と呼べるか失敗と呼べるか等、$challenge$の性質等に応じて適宜定められた客観的な尺度です（したがって、厳密にいえば、関数$f$はあらゆるケースにおいて通じる固定的な関数ではなく、$challenge$の対象の性質によって適宜定められる関数です。例として、営業利益のために努力したのであれば、営業利益の尺度に基づく評価でアウトプットの値が決定されてもよいでしょう）。決定される評価は、その尺度において「悪い」と判断される場合にはマイナスが付されます。

なお、"ある特定の尺度"は１つであるか複数であるかは問いません。１つであれば、$f(challenge)$は実数のスカラーで表されることになるでしょう。複数であれば、$f(challenge)$は実数を成分とするベクトルで表されることになるでしょう。

右辺は、$f(challenge)$に絶対値（またはノルム）を表す記号"$｜｜$"がつくことによって、$f(challenge)$が表している、"ある特定の尺度（１つか複数かは問わない）における評価"が、「マイナスの評価」を意味するものであっても、それはプラスになる、ことを意味しています。

これより、全体としてこの数式が意味するところは、「ある挑戦が、ある尺度において悪い結果をもたらしたと判断されるものであったとしても、挑戦したこと自体はプラスの価値になるのだ」ということになります。
もちろん、むやみやたらに挑戦をすればいいというわけではありません。良い成果を求めてfeelし、thinkし、imagineした（２つ目のコアバリュー参照）上での$challenge$であることが前提です。また、この式は値の大小について重視した式ではなく、「$Value$の値が大きくなるような挑戦を選んで行え」といった意味は込められていないということは、念のためここに付言しておきます。

左辺の"$Our$ $Work$"は会社、個人またはチームが仕事でアウトプットする成果のことを示しています。この式では私たちのアウトプットする成果がどのような過程を経て出来上がるのかを示しています。

右辺の極限の中身の関数$W(f,t,i)$は、feelした度合い"$f$"、thinkした度合い"$t$"、imagineした度合い"$i$"をパラメータとし、成果を返す関数です。この関数は、具体的な仕事についてそれぞれ定義されるものと考えられるため、厳密には添字"$j$"などを付して$W_j(f,t,i)$とするのが正確かもしれませんが、暗黙的に省略しています。なお、返り値は例えば実数値や整数値で、"膨大な取り得るオプションの中から出した１つの答え"というイメージです。
feel(感じる)とは、向き合っている仕事やプロジェクトにおいて、五感を駆使して、自分の中に抱く純粋な感情を引き出すこと、think(考える)とは、認知、インプットした情報を元に、適切な解や方針を見つけようと模索すること、imagine(想像する)とは、ここでは、自分と異なる環境や立場・考え方に対して思いを馳せることを意味しています。
今回、$f,t,i$は、feel,think,imageした度合いであるので、実数値であり、限りなく大きくとることができる値であることを想定しています。
$\lim\limits _{f,t,i\ \to\ \infty }$は、限りなくfeel,think,imagineすることを意味しており、右辺全体は、無限にfeel,think,imagineしたときの成果のことを示しています。

式をそのまま解釈すると、無限にfeel,think,imagineした上のアウトプットが理想であるということになります。ここに込められたメッセージとしては、世界中の子どもに届けられるコンテンツを作るために組織が大切にしたいのが、有限な時間の中でも可能な限り感じて考えて想像し尽くしてアウトプットすることである、ということです。

なお、数学的には、$\lim\limits _{f,t,i\ \to\ \infty } \ W( f,t,i)$という表現は、「$f,t,i$を無限にしたとき、進路に関わらず$W(f,t,i)$は一点に収束する」という意味を内包していますが、$f,t,i$の無限への飛ばし方によっては、$W(f,t,i)$の収束値が異なる可能性があるとも考えられます。人によってはfeelの度合いがthinkよりも多くアウトプットが違ってくるということがあってもよいでしょう。この考えに数式が矛盾しないようにすると、右辺は、$n$という媒介変数を用いて $\lim\limits _{n \to\ \infty} \ W(f_{n},t_{n},i_{n})$と表すのが、より適切かもしれません。このとき、$f_{n},t_{n},i_{n}$は$n$に依存して変化する値であり、$n→∞$のとき、$f_{n}=\infty,t_{n}=\infty,i_{n}=\infty$となるような値です。人や時代によって、$f_{n},t_{n},i_{n}$が$n$にどのように依存するかは決められることになります。

"$a_{n}$"は自分を構成するものであり、$a_{n+1}$"は未来の自分を構成するものです。あるタイムスパンを想定し、その前後を"$n$","$n+1$"で表しています。簡易解説では"$a_{n+1}$"を「明日の自分」とみなして記載していますが、必ずしも常に１日というタイムスパンで考えなくてもよく、１時間でも、１週間でもよいでしょう。

式は、自分に$Σ|\vec{I} \times \overrightarrow{U_{x}}|$が足されることで未来の自分が作られる、ということを表しています。つまり、より良いコンテンツを生み出していくため、積極的に$Σ|\vec{I} \times \overrightarrow{U_{x}}|$を大きくして自分の価値観をアップデートしていこう、というメッセージが、この式には込められています。

$n$から$n+1$までの時間において新たに認知されたある情報 （$\overrightarrow{U_{x}}$）に対し、個人の興味や関心に応じたアンテナ（$\vec{I}$）が作用することで、自分はアップデートされます。アップデートの程度は、"$|\vec{I} \times \overrightarrow{U_{x}}|$"で表され、これは、二つのベクトルが張る平行四辺形（図１）の面積を意味します。つまり、二つのベクトルが張る平行四辺形の面積が大きければ大きいほど、アップデートの程度が大きくなる、ということになります。
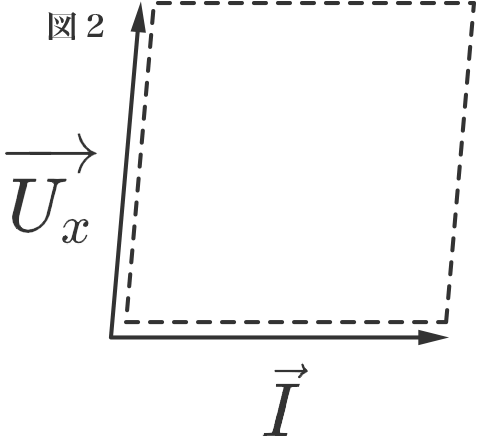
自分の持つアンテナの方向性に近い情報を認知した場合には、図1のように、平行四辺形の面積はさほど大きくはなりません。逆に、自分の身近にいない人の価値観や新しいテクノロジーに関する知見など、今まで自分の持っていたアンテナとは異なる方向性の情報を取り入れると、平行四辺形の面積は大きくなります（図２）。すなわち、興味のあることばかりではなく、知らない世界にも積極的に飛び込んでいけば、知見はさらに広がり、自分は大きくなっていける、ということになります。

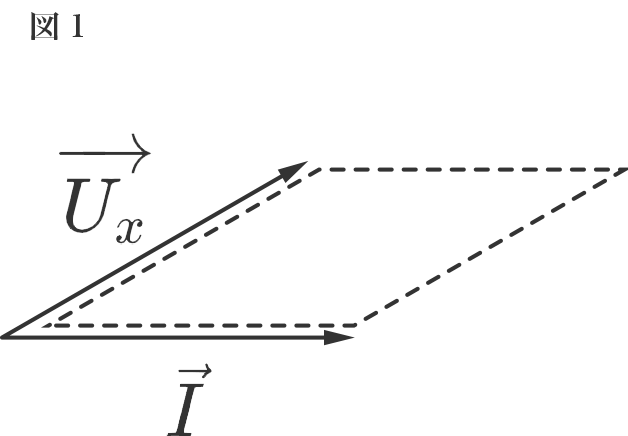
ちなみに、自分のアンテナが指す方向と正反対の思想に触れた場合はどうでしょうか。"正反対"というと、$\vec{I}$とは180度違う方向を向いたベクトルになるように思われますが、実際は、「正反対の思想の人がいる」「そういう考え方もある」という事実も含めれば、その情報が表す$\overrightarrow{U_{x}}$は必ずしも$\vec{I}$の真逆方向を向いているわけではないといえます。すなわち、$|\vec{I} \times \overrightarrow{U_{x}}| = 0$ となるのはよほど特殊なケースであり、大抵の場合は（自分の思想と正反対の思想に触れた場合であっても、）$|\vec{I} \times \overrightarrow{U_{x}}|$ は正になるといえるでしょう。

なお、外積は、本来、任意の次元のベクトルに対しては定義できないため、厳密には、先述した「二つのベクトルが張る平行四辺形の面積」として表現するのが適切とは思われますが、今回はコアバリューとしてのシンプルさを優先し、外積として表現しました。ベクトルの表記も、本来は「$\boldsymbol{ I }$」のように、太字で表すことが慣例とされますが、わかりやすさの観点から今回の表記を採用しています。また、"$\vec{I}$"も自身の成長とともに変化していくはずのベクトルであり、"$\overrightarrow{I_{n}}$"と表記するのがより適当ではありますが、表記を簡明にするため、自明のものとして記載を省略しています。

ところで、"$a_{n}$" は、「個人を構成するもの」を表しますが、個人のみならず、組織にも当てはめることができます。その時代その時代においてできる最高のアプローチをしていくために、組織としても、つねに新しいものを取り入れて成長していきたいと考えています。